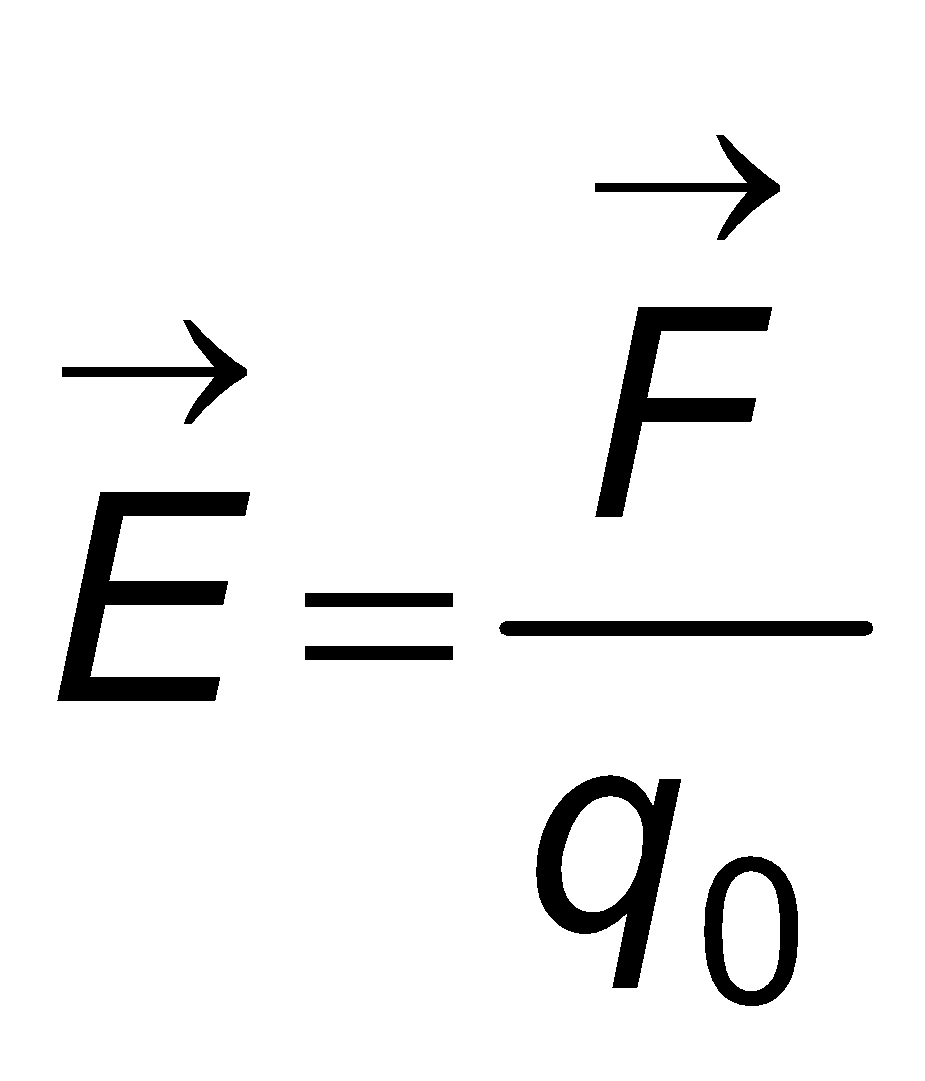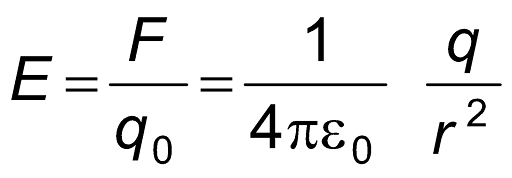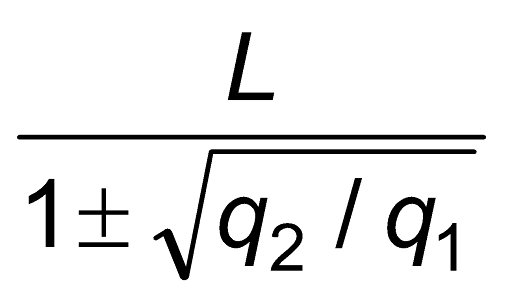ELECTRIC FIELD

The concept of an electric field entails a designated area wherein the presence of a charge would result in the exertion of a force. When an electric charge is introduced into an electric field, it undergoes a force.

The electric fields that will be examined in this study are typically generated by various forms of charged entities, such as point charges and charged plates. The topic of discussion pertains to a charged sphere and related concepts. The electric field of a charged body can be defined as the spatial domain in which it exerts a force on other charges, thereby exerting its influence.

When two point charges are positioned as depicted, the forces acting upon them can be described in two distinct manners.The charge q2 is situated within the electric field generated by the charge q1.

1. Therefore, the electric field generated by charge q1 applies a force on charge q2.

2. The electric field of charge q2 influences the charge q1. Consequently, the charge q2’s electric field applies a force on q1.

The electric field is responsible for exerting a force on charges that reside within its domain. The generation of an electric field is attributed to the presence of charged entities.

5.1 Electric Intensity or Electric Field Strength

The electric field intensity at a given point within an electric field refers to the magnitude of the force exerted on a hypothetical unit positive charge positioned at that specific point. This assumption is made under the condition that the presence of the unit charge does not have any influence on the electric field itself.

Therefore, if a test charge with a positive value q0 undergoes a force Vector F at a specific location within an electric field, the electric field intensity Vector E at that particular point can be determined using the following equation: 

Several key aspects related to electric power should be considered.

(i) Intensity is a vector quantity. The orientation of the electric field intensity at a given location within the electric field corresponds to the direction in which the electric field applies a force on a unit positive charge.

(ii) The dimensions of the electric field intensity 

               In S.I. systems, the unit of is N/C or V/m as

                          =

5.2       Forced Exerted By a Field on a Charge Inside It

               By definition as 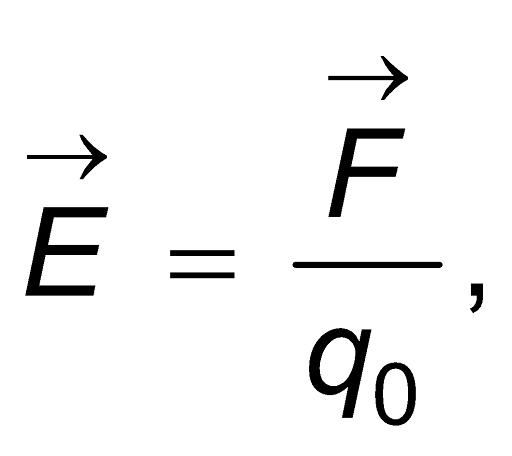i.e.,

               If q₀ is a +ve charge, force  on it is in the direction of .

               If q₀ is a –ve charge,  on it is opposite to the direction of

Question:       An electron (q = – e) is placed near a charged body experiences a force in the positive y direction of magnitude 3.60 × 10^–8 N.

            (a)        The electric field at that location is x * 10^–9, find x. (where x is in N)

            (b)        What would be the force exerted by the same charged body on an alpha particle
(q = +2e) placed at the location initially occupied by the electron?

Solution:        Using equation (7), we have

                         = 225   

                        The electric field is in the negative y direction.

            (b)        The force on the alpha particle is given by

                        F_y = q₀ E_y = 2(+ 1.60 × 10^–19 C) (2.25 × 10¹¹ N/C)  =  72

                        The force is in the negative y direction, the same direction as the electric field.

5.3 The electric field intensity resulting from a point charge.

Consider a scenario where a test charge with a positive value, denoted as q0, is positioned at a radial distance r from a point charge q. The magnitude of the force exerted on q0 can be determined using Coulomb’s law.

The magnitude of the electric field at the location of the charge is.

The direction of Vector E coincides with the direction of Vector F, both of which align along a radial line originating from q. This radial line extends outward when q is positive and inward when q is negative.

The provided diagram illustrates the orientation of the electric field vector E at multiple locations in close proximity to a positively charged point.

5.4 The Calculation of Electric Field Intensity Arising from a Collection of Point Charges

The principle of linear superposition, which holds true for Coulomb’s law, is likewise applicable to the electric field. In order to determine the magnitude of the electric field at a specific point resulting from a collection of N point charges.

The initial step involves determining the respective magnitudes of the individual field strengths. The vector E1 represents the electric field due to the presence of Q1, while the vector E2 represents the electric field due to the presence of Q2, and so forth.

The resulting field strength is determined by the vector sum of the individual field strengths.

  = ∑ (n = 1, 2, 3, … N) 

Question:       A point charge q₁ of + 1.5 μC is placed at a origin of a co-ordinate system, and the second charge q₂ of + 2.3 μC is at a position x = L , where L = 13 cm. At what point P along the x-axis is the electric field zero (in mm).             

Solution:        The point must lie between the charges because only in this region the forces exerted by q1 and q2 on a test charge oppose each-other. If is the electric field due to q1 and  is that due to q2, the magnitudes of these vectors must be equal, or

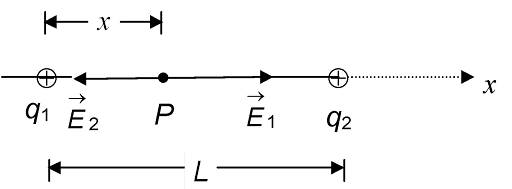
                                    E₁ = E₂

                                        We then have

,where x is the co-ordinate of the point P. 

                        Solving for x, we have

                                    x =

                        Substituting numerical values for L, q₁ and q₂,

                        We obtain

                                    x = 5.8 cm and x = – 54.6 cm

                        But the negative value of x is unacceptable

            Hence, x = 58 mm