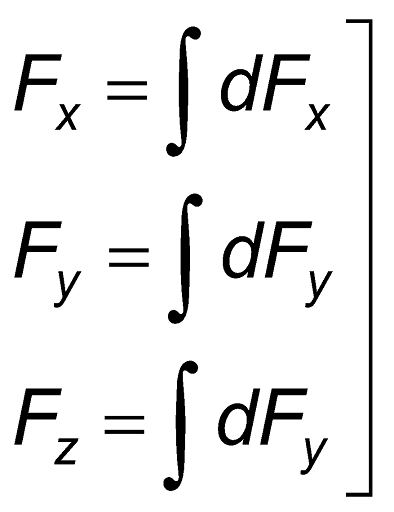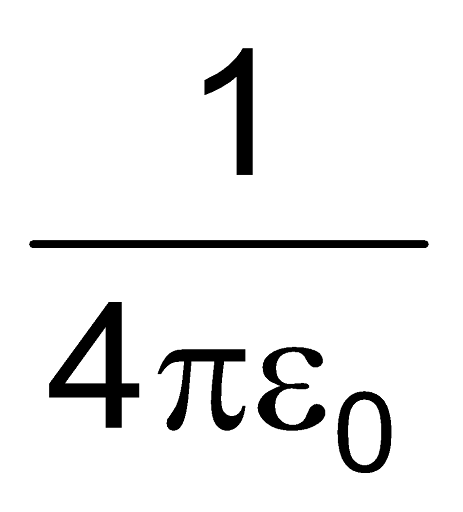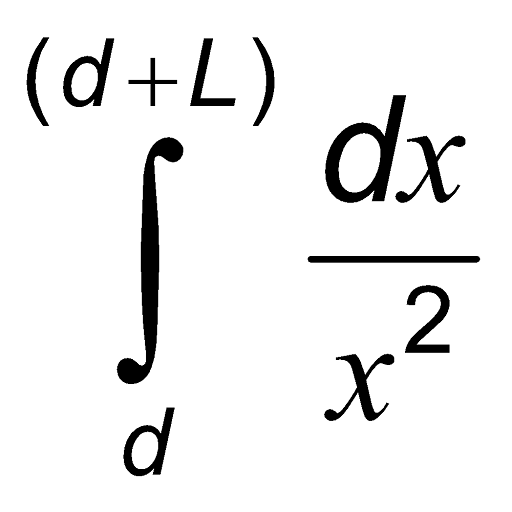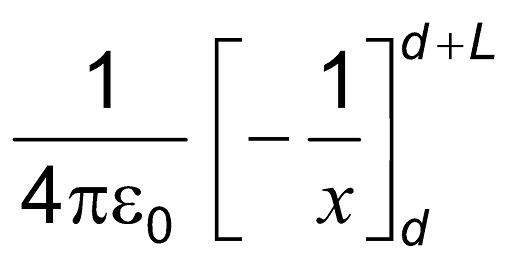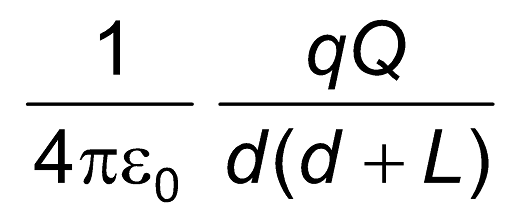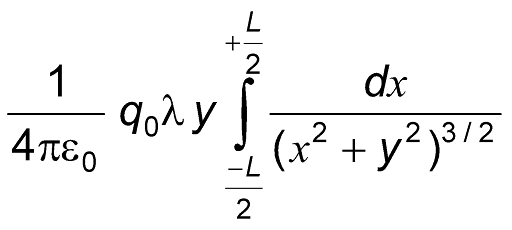FORCE DUE TO CONTINUOUS CHARGE DISTRIBUTIONS
In order to determine the force exerted by a continuous charge distribution on a point charge, it is necessary to partition the charge into infinitesimally small charge elements. Subsequently, every infinitesimal charge element is regarded as a point charge.
The equation provided expresses the magnitude of the force, denoted as dF, exerted by the charge dq on the charge q0.
This force is determined by the distance, r, between the charges dq and q0. The determination of the total force entails the summation of all infinitesimal force elements, necessitating the utilization of an integral.
Taking , we have
Due to the inherent vectorial properties of integration, it is imperative to execute the mathematical procedure with meticulous attention. The simplification of calculations is often facilitated by the presence of symmetry in the distribution of charges.
The table provided below presents a description of each type of charge distribution, accompanied by its corresponding Greek letter parameter: λ, σ, or ρ.The selection of the charge element dq is contingent upon the specific characteristics of the charge distribution.
| Charge distribution | Relevant parameter | SI units | Charge element dq |
| Along a line | λ, charge per unit length | C/m | dq = λ dx |
| On a surface | σ, charge per unit area | C/m2 | dq = σ dA |
| Throughout a volume | ρ, charge per unit volume | C/m3 | dq = ρdV |
| Question: A point charge q is situated at a distance ‘d ’ from one end of a thin non-conducting rod of length L having a charge Q (uniformly distributed along its length) as shown. Find the magnitude of the electric force between the two. (in N) (take q = 10–6C, Q = 9 × 10–3C, d = 1m, L = 2m) | |
| Solution: Consider an element of rod of length ‘dx ‘ at a distance x from the point charge q. Treating the element as a point charge, the force between q and the charge element will be | |
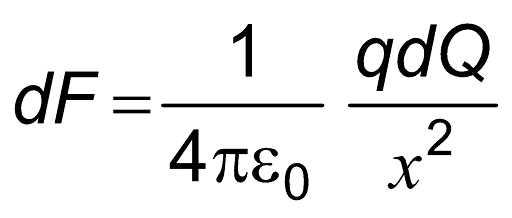
But dQ = dx
So, dF =
∴ F =
=
=
=
= 27
| Question: A thin non-conducting rod of length L and having a charge Q (uniformly distributed along its length) is placed along x-axis, as shown. Find the force (in N) exerted by the rod on the point charge q0 located on the perpendicular bisector of the rod (the positive y-axis) at a distance y from the centre (take y =1m, L = 2m, q0 = √2 × 10–6C, q= 9 × 10–3 C.) |
| Solution: Consider an element of rod of length ‘dx ‘ at a distance x from the centre. Treating the element as a point charge, the force between q and the charge element will be The direction of So, For every charge element dq located at position +x, there is another charge element dq located at –x. When we add the forces due to the charge elements at + x and – x, we find the x components have equal magnitudes but point in opposite directions. So their sum is zero, i.e., Fx = 0 |
Now, dFy = dF sin θ
=
(∴ r2 =x2 + y2; sin θ = )
or, dFy =
∴ Fy = ∫dFy =
Evaluating the integral, we obtain
Fy =
= 81